
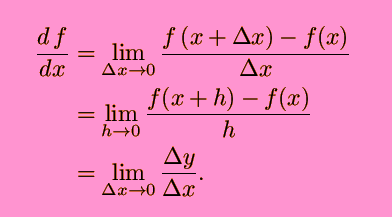
Geometrically, the derivative at a point is the slope of the tangent line to the graph of the function at that point, provided that the derivative exists and is defined at that point. The process of finding a derivative is called differentiation. The derivative of a function at a chosen input value describes the rate of change of the function near that input value.

The primary objects of study in differential calculus are the derivative of a function, related notions such as the differential, and their applications. It is one of the two traditional divisions of calculus, the other being integral calculus-the study of the area beneath a curve. Of a point in rectilinear motion according to the law $ s = f ( t) $.In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change.

10 Derivatives and differentials of composite functions.īe defined in some neighbourhood of a point $ x _ ( t) $.9 Differential calculus of functions in several variables.8 Principal theorems and applications of differential calculus.3 Mechanical interpretation of the derivative.2 Geometric interpretation of the derivative.The central concepts of differential calculus - the derivative and the differential - and the apparatus developed in this connection furnish tools for the study of functions which locally look like linear functions or polynomials, and it is in fact such functions which are of interest, more than other functions, in applications. Differential calculus is based on the concepts of real number function limit and continuity - highly important mathematical concepts, which were formulated and assigned their modern content during the development of mathematical analysis and during studies of its foundations. Differential calculus is usually understood to mean classical differential calculus, which deals with real-valued functions of one or more real variables, but its modern definition may also include differential calculus in abstract spaces. The creation of differential and integral calculus initiated a period of rapid development in mathematics and in related applied disciplines. Leibniz towards the end of the 17th century, but their justification by the concept of limit was only developed in the work of A.L. Differential and integral calculus were created, in general terms, by I. Descartes was the principal factor in the creation of differential calculus. The introduction of variable magnitudes into mathematics by R. Together they form the base of mathematical analysis, which is extremely important in the natural sciences and in technology. The development of differential calculus is closely connected with that of integral calculus. A branch of mathematics dealing with the concepts of derivative and differential and the manner of using them in the study of functions.


 0 kommentar(er)
0 kommentar(er)
